Spherical Harmonics Lighting

1. The Spherical Harmonics Basis

1.1 Spherical Harmonics Mathemactics

Harmonics functions is a solution of Laplace function, which is a series of orthogonal basises.

The relation between polar coordinates and cartesian coordinate is as follows.

1.3 Projection from Cubemap

Irradiance map is an essential part in Image based Rendering. To reduce the storage cost, we can project the irradiance map to a series of spherical harmonics parameters. In the real-time applictaion, we can rebuild the irradiance based on the harmonics parameters. Analytic solutions exist for the first several orders of spherical harmonics.

2. The Global Illumination in Modern Game Engine

2.1 The Modern Shading Pipeline

In this chapter, we will discuss about how the global illumination can be used in shading pipeline. As we all know, different shading models have different BRDF functions, which means these shaders’ calculation are different with each other. To embed the global illumination in the shading pipeline, we separate the shading process into two parts in architecture view: direct lighting and environment lighting.

• Direcet Lighting: the direct shading process contains the direct diffuse and direct specular.
• Environment Lighting: the indirect shading process contains the environment diffuse and environment specular.
  • the environment diffuse generated by the lights probe in game engine.
  • the environment specular generated by the reflection probes, SSR, reflection planar probes.

In the custom game engine, we can design the shader architecture as follows. We focus on the environment diffuse calculation in this blog.

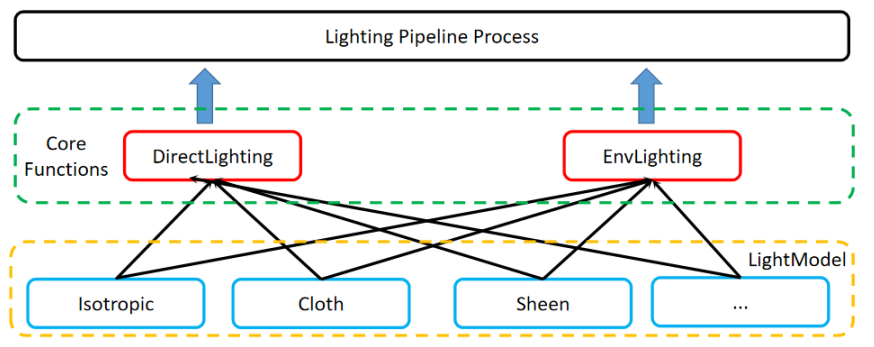
2.2 The Light Probes Conceptions

The spherical harmonics are suitable for storing the low-frequency information. Hence, the diffuse lighting information with low-frequency can be projectted into the spherical harmonics.

3. Light Probe Baking

3.1 Conception

The process of calculating spherical harmonics for each light probes is called baking.

After baking, to shading a fragment, we interpolate the spherical harmonics value based on the position of current fragment. The process:

(1) We interpolate the sh values in the light porbes volume based on the normal vector and world space position of current fragment.

(2) This sh value can be encapsulated in the structure to send to the shading pipeline.

(3) Furthermore, we can get the indirect environment diffuse by multiplicating of sh values and albedo.

Albedo refers to the diffuse color of a material or surface, which is the color that is scattered equally in all directions when light hits it.

3.2 Cubemap Generation

As we all know, the irradiance map indicate the environment diffuse lighting around the current position. So, we need to record the environment diffuse light state to get accuracy environmental diffuse lighting.

In modern game engine, we place multiple probes around the scene. Each light probe stores the spherical harmonics parameters, which are the projection of the surrounding diffuse lighting information(cubemaps/samples). The diffuse lighting information can be gained through two ways:

• Cubemaps: Take pictures in six directions of cubemaps from the probe view.
  • we need to real-time capture multi-times to gain a cubemap with multi-bounce lighting effect.
• Samples: Each texel in cubemap can be recognized as a sample result in target direction.
  • We can send the direction to a off-line ray tracer to get the rendering result.

Above all, we have got the cubemap/samples of current position right now.

3.3 Probe Baking Theory

In the baking process, we should projected the cubemap to a series of spherical harmonic parameters.

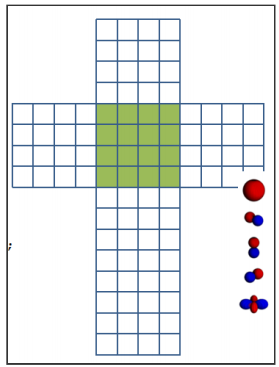
The above figure shows the rebuild results for different orders spherical hamonics parameters. If we use the higher orders spherical harmonics parameters, we can get the accurate rebuild results. However, we need more space to store the parameters. It’s a trade-off between performance and effectiveness. Always, we choose 3 orders spherical harmonics parameters to store the diffuse environment lighting.

We can use the following process to project the cube map to a 3 order spherical harmonics parameters, which come from the paper Stupid Spherical Harmonics.

There are some key points that we need to be clear.

• The t(texel) is the color of current texel;
• EvalSHBasis is the function to get the SH Basis Function based on current texel’s information.
• The calculation of fTmp and fWt is to calculate the differential solid angle.
• The final result divided by fWtSum/4π, which means the spherical integral.

The EvalSHBasis is the essential part to baking the environment diffuse lighting. The EvalSHBasis function solve current SH Basis based on the direction vector of related texel. As the following figure, each texel has their own SH basis values.

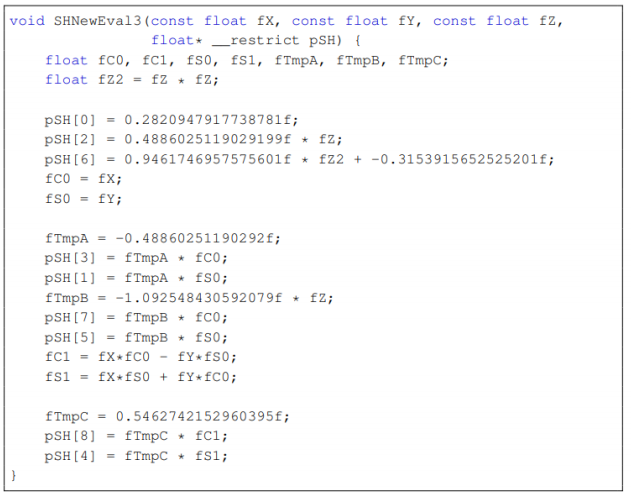
There is one implementation of EvalSHBasis function, which comes from paper Efficient Spherical Harmonic Evaluation(https://jcgt.org/published/0002/02/06/paper.pdf). By the following implementation, we can evaluate the 3 order spherical harmonics parameters rapidly. To be honest, I dont know the theory about the implementation, but it works really well.

3.4 The Baking Architecture Implementation

In this section, we discuss about the implementation of the section 3.3. In mordern game engine, there always have the conception of Render Pass. The most important thing is that we should decrease the number of render passes. The interaction between the CPU and GPU is really high, the decreasing of the render passes can significantly increase the efficiency.

So we use the Mipmap generation process to boost the evaluation process of SH parameters. We can implement this process in the Computer Shader of DirectX12. For brevity, we just talk about the algorithm steps but no implementation. You can implement the sh probes baking by any graphics api.

3.4.1 SH Cubemaps Calculation

In the probe baking process, we need to calculate the 9 SH parameters. Considering about the efficency, we calculate the 9 SH parameters separatly.

In the engineering view, to achieve the goal of SH Projection effectively, we should try to put the same calculation in the same render pass.

So, in the first stage, we need to calculate 9 cubemaps for related 9 SH parameters. Each texel in the cubemaps is calculated as follows:

The implementation in game engine, we can write the rendering structure like the following architecture.

Texture outputSHCubeMaps[9][6];
for(int shIndex = 0; shIndex < 9; shIndex++)
{
    for(int cubemapIndex = 0; cubemapIndex < 6; cubemapIndex ++)
    {
        Renderpass SHCubeMapGenerationPass;
        SHCubeMapGenerationPass.CalculateSHCubeMap(shIndex, cubemapIndex, &outputSHCubeMaps[shIndex][cubemapIndex]);
    }
}

In this way, we can generate a 2 dimension texture array outputSHCubeMaps, which means that each sh parameter corresponds a sh values cubemaps. Each cubemap has 6 two-dimension texture.

In the CalculateSHCubeMap function, we use the pixel shader in DirectX12 to implement the fragment calculation.

//1. SH pre-calculation
//get the uv value(-1~1) based on the origin uv value(0~1)
float2 uv = origin_uv * 2 - 1;
//calculation based on the Stupid Spherical Harmonics
float fTmp = 1 + u^2 + v^2;
float fWt = 4 / (sqrt(fTmp) * fTmp);
EvalSHBasis(texel, s);

//2. texel sampling
//from the texture uv to cube map coordinates
float3 cube_map_uv = Mapping2Cubemap(uv);
//sample the environment cubemap texel
float3 environment_color = environmentCubeMap.Sample(Sampler, normalize(cube_map_uv));

//3. output the fragment
float4 output = float4(environment_color * fWt * s[shIndex], fWt);

3.4.2 Spherical Integral Calculation

Then we use the mipmap mechanism to evaluate the spherical integral.

Texture SHCubeMapsWithMipmaps[9][6][9];
for(int shIndex = 0; shIndex < 9; shIndex ++)
{
    for(int cubemapIndex = 0; cubemapIndex < 9; cubemapIndex++)
    {
        ComputePass mipMapPass;
        mipMapPass.GenerateMipmaps(shIndex, cubemapIndex, &SHCubeMapsWithMipmaps[shIndex][cubemapIndex]);
    }
}

float finalSH[9];
for(int shIndex = 0; shIndex < 9; shIndex++)
{
    ComputePass weightPass;
    weightPass.weightSHParameters(shIndex, &finalSH[shIndex]);
}

In the first loop, we generate the mipmap based on the output sh cubemaps generated in section 3.4.1.

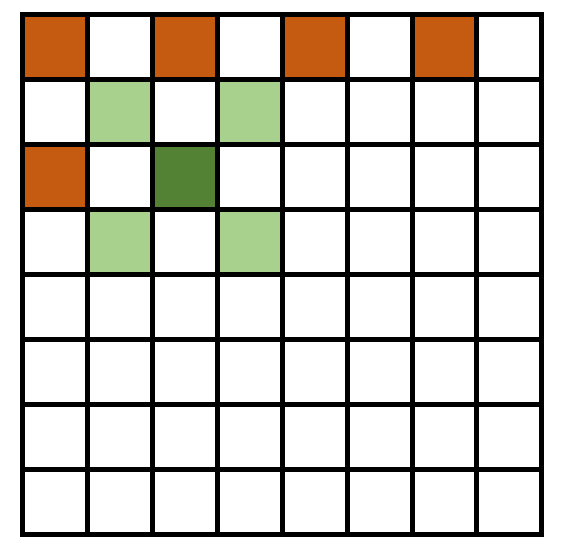
It is worth mentioning that the mipmap generation progress has another better choice. As the following figure show, the red pixels are processed. The dark green pixels is generated by average the values of the reseda pixels. By this way, we can increase the continuity of the generated mipmaps.

Finnaly, we average the level 8 mipmap texture(only one pixel). The weightSHParameters function is as follows:

float4 weightValue = float4(0.0);
for(int i =0; i < 6; ++i)
{
    weightValue += SHCubeMapsWithMipmaps[shIndex][i][8];
} 

finalSH[shIndex] = 4 * π * weightValue.xyz / weightValue.w;